Atividades de Matemática(05/10 a 16/10) 3º EM A/ B - Prof.º João
- Escola Lydia Yvone

- Oct 8, 2020
- 2 min read
Equações e inequações
Equação é uma igualdade (=) envolvendo uma ou mais incógnitas. E inequação é uma sentença matemática expressa por uma desigualdade – através dos símbolos: ≠ (diferente de), < (menor que), > (maior que) , ≤ (menor ou igual a), ≥ (maior ou igual a) -, relacionando uma ou mais variáveis. Ambas são usadas para resolver problemas, são a tradução para a matemática de um problema em linguagem corrente.
Grau de uma Equação e de uma Inequação
Tanto a equação como a inequação têm o mesmo grau do monômio de maior grau de sua sentença. Por exemplo, a equação x³+2x+5 é de terceiro grau porque seu monômio de maior grau é x³ e a inequação x²-1 < 0 é de segundo grau porque seu monômio de maior grau é x².
Equação do Primeiro Grau
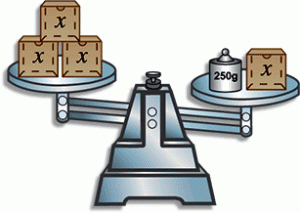
Para resolver uma equação do primeiro grau, passamos o problema para a linguagem matemática, depois isolamos a variável e, então, encontramos seu valor.

No exemplo acima, temos uma balança em equilíbrio, logo:
Portanto, x = 150g.
Inequação do Primeiro Grau
Como fizemos na equação, para resolver uma inequação do primeiro grau, também passaremos o problema para a linguagem matemática e isolaremos a variável, porém, não descobriremos seu valor e sim uma informação sobre ele que nos permitirá dizer o conjunto ou o intervalo de valores que satisfaz nossa inequação.
Continuando com o problema da balança, agora temos uma situação em que ela se encontra desequilibrada. Como podemos ver, o lado direito está mais pesado que o esquerdo, assim:
Como x não pode ser um número negativo, já que representa a quantidade de gramas de determinado objeto, o intervalo que satisfaz nossa inequação sendo x um número real é [0, 125).
Equação do Segundo Grau
É a equação escrita sob o formado ax²+bx+c, sendo a ≠ 0. Pois se a=0, a equação volta a ser do primeiro grau. Para achar a solução dessa equação usamos a famosa fórmula de Bhaskara, que foi justificada no Resumo de Função Quadrática.
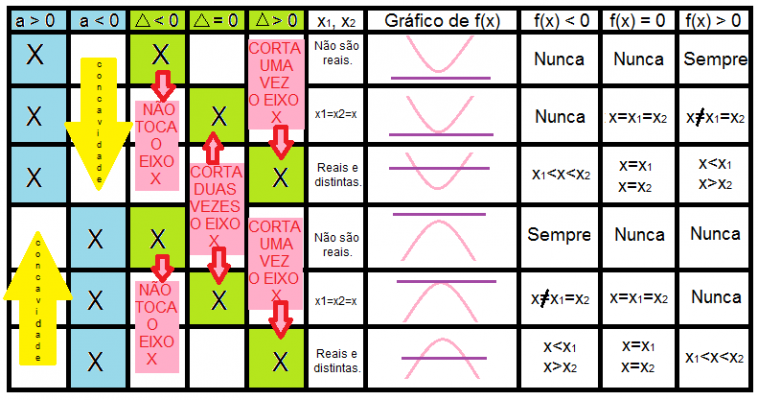
Inequação do Segundo Grau
Sendo a ≠ 0, são inequações do segundo grau as sentenças abaixo:
i) ax² + bx + c > 0 ii) ax² + bx + c < 0 iii) ax² + bx + c ≥ 0 iv) ax² + bx + c ≤ 0 v) ax² + bx + c ≠ 0
Resolver essas equações é responder se existe x tal que f(x) = ax² + bx + c seja:
i) positiva ii) negativa iii) não negativa iv) não positiva v) não nula
A resposta se encontra no estudo do sinal de f(x) e pode ser feito através do gráfico da função.
Exercícios:
1- "O preço de uma caneta é o dobro do preço de uma lapiseira e as duas juntas custam 30 reais." Usando as incógnitas x e y, qual dos sistemas de duas equações de 1° grau abaixo representa o que deve ser feito no problema acima?
a) x = 2y e x + y = 30
b) x = 2y e x - y = 30
c) x + 2y = 30 e x = 4y
d) x = 2y e x + 3y = 30
2- Qual é o valor de N na inequação a seguir: -8n + 3501 > 210 – 5n ?
a) n = 1097
b) n < 1097
c) n > 1097
d) n = 1095


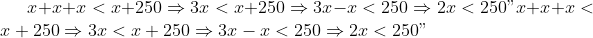



Comments