Volume de cilindro reto e medidas de capacidade
O cilindro é um sólido geométrico classificado como corpo redondo por conter uma de suas faces arredondadas. Podemos observar a utilização do cilindro na indústria de embalagens, reservatórios de combustíveis e líquidos em geral. Em virtude da sua grande utilização no cotidiano, é importante conhecer seus elementos e saber realizar o cálculo de seu volume.
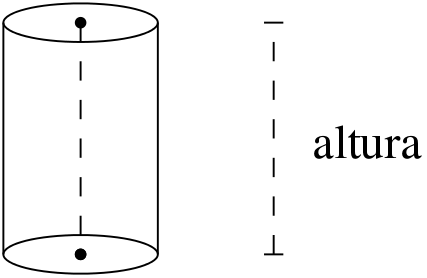
Considere um cilindro circular reto de altura h e raio da base r. O volume do cilindro é obtido realizando o produto entre a área da base e a altura h. Ou seja,
V = (área da base) × (altura)/ V = Ab·h → V = π·r²·h
Como a base do cilindro é uma circunferência de raio r, temos que:
(área da base) = π x r²
Sabemos que a altura do cilindro é h. Assim, a fórmula para o cálculo do volume do cilindro é dada por:
V = π.r².h
Sendo r → o raio da base. h → a altura do cilindro.
Esse tipo de sólido geométrico é muito utilizado no cotidiano como reservatório de substâncias liquidas e gasosas.
Quando trabalhamos com sólidos geométricos, precisamos relembrar as principais relações entre as medidas de volume e de capacidade. Veja:
1 m³ (metro cúbico) = 1 000 litro
1 dm³ (decímetro cúbico) = 1 litro
1 cm³ (centímetro cúbico) = 1 ml Vejamos alguns exemplos de aplicação da fórmula do volume do cilindro. Exemplo 1. Considere um cilindro circular reto de 8 cm de altura e raio da base medindo 5 cm. Determine a capacidade desse cilindro. (Utilize π = 3,14) Solução: De acordo com o enunciado do problema, temos que: h = 8 cm r = 5 cm Calcular a capacidade é o mesmo que determinar o volume do cilindro. Utilizando a fórmula do volume, obtemos: V = π.r².h V = 3,14 x 5²x8 V = 3,14 x 25 x 8 V = 628 cm³ Portanto, esse cilindro apresenta capacidade de 628 cm³. Exemplo 2. Um reservatório de combustíveis apresenta o formato de um cilindro circular reto de 15 metros de diâmetro e 6 metros de altura. Determine a capacidade, em litros, desse reservatório. (Utilize π=3,14)
Solução: Temos que: r = d/2 = 15/2 = 7,5 m h = 6 m Utilizando a fórmula do volume, obtemos: V = π.r².h V = 3,14 x (7,5)² x 6 V = 3,14 x 56,25 x 6 V = 1059,75 m³ O exercício quer a capacidade em litros. Devemos lembrar que: 1dm³ = 1 litro ou 1m³ = 1000 litros Assim, o volume, em litros, desse reservatório será de: V = 1059,75 x 1000 = 1.059.750 litros Exemplo 3. Uma indústria de embalagens deseja fabricar uma lata de tinta cilíndrica com raio da base medindo 5 cm de comprimento e com capacidade para 1 litro. Qual deverá ser o comprimento da altura dessa embalagem? (Use π = 3,1)
Solução: De acordo com o problema, o volume desse cilindro deverá ser de 1 litro ou 1 dm³. Sabemos que o raio da base será de 5 cm, que equivale a 0,5 dm. Utilizando a fórmula do volume, teremos:
Portanto, a lata deverá ter uma altura de, aproximadamente, 13 cm.
Agora por fim, segue a atividade desta aula, boa semana a todos.
Comments